斜辊矫正钢管圆度变化规律-斜辊矫正钢管圆度变化规律的研究
在弹塑性弯曲矫正理论的基础上,对2-2-2型矫正机的矫正过程进行了分析。结果显示了各辊的矫正效果以及压扁量的最佳选择区间,为提高矫正精度、制定最优矫正工艺提供了理论依据。关键词:钢管圆度,压扁量,弹塑性变形,残余曲率
随着石油、航空、航天等工业技术的发展,对钢管圆度的精度有越来越高的要求。斜辊矫正机作为钢管圆度控制的辅助手段发挥着重要作用。如何设置压扁量,有效控制钢管的圆度,对产品的质量会有不同的影响。目前制定的规程和原则仍处于经验之中。国内已有部分技术人员从理论上进行了基础研究,对进一步认识压扁量的作用及如何设定压扁量提供了基础理论。为了进一步了解矫正过程的变化规律,本文在弹塑性变形理论研究的基础上对各设定参数的变化关系进行了研究。通过分析可以进一步掌握压扁量与圆度控制精度之间的相互关系,为制定合理压扁量提供理论依据。
1.钢管弹塑性变形基本理论
1.1基本假设[1]
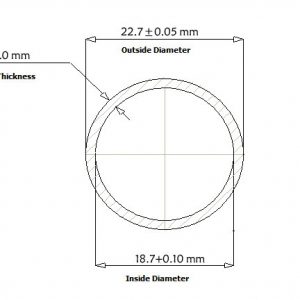
由于钢管矫正温度较高,因此可以认为管材为理想弹塑性体。钢管在矫正时仅受上下矫正辊集中载荷的作用。管材受压变形后为近似椭圆形,且中心轴与壁厚的中心线相重合,符合平面截面假设。钢管压扁矫正模型如图1所示。
1.2弹塑性矫正变形的理论
1)设钢管标准原始曲率为1/ρ0,则被矫钢管在矫正辊的作用下将产生弹塑性变形,弯曲力矩与曲率变化量的关系为[2]:
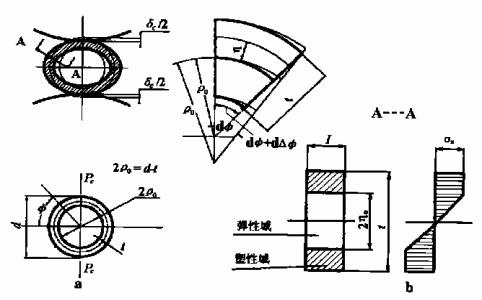
图 1 钢管的压扁矫正模型
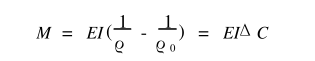
式中ΔC为曲率变化量,1/mm;E为材料的弹性模量,MPa;I为截面惯性矩,mm4;ρ0=(d-t)/2,mm;1/ρ为弯曲曲率,1/mm。弹塑性弯曲变形力矩方程为:
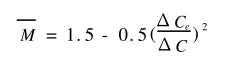
式中M为相对弯矩;ΔCe为屈服曲率变化量,其值为2σsEt,1/mm。
设圆环断面的弹区比为ζ,则
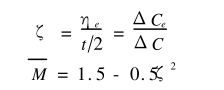
2)弹性极限压扁量δce,相对压下系数η[3]。
钢管轧件的弹性极限状态是轧件弹塑性变形的初始起点。为了分析不同的压扁量对矫正质量的影响,需要确定初始压扁量的大小。由于轧件仍处于弹性状态,根据弹性变形时功能相等的原理求解标准钢管压扁时δce。
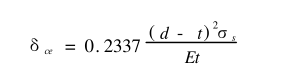
式中d为钢管的公称外径,mm;t为钢管的壁厚,mm;σs为轧件的屈服极限,MPa。
η=δc/δce
式中δc为实际压扁量,mm;η为相对压下系数。
3)管材原始曲率变化量(1/mm)。
设管材矫正前为椭圆形,长短轴的直径差为Δd,则管材的原始曲率相对标准管材的原始曲率变化量:

4)反弯曲率变化量(1/mm)。
根据文献[4]可知管材在压扁时水平方向与垂直方向的压扁量之比值近似等于0.92。因此钢管在矫正时设压扁量为δc,则矫正时反弯曲率相对标准管材的初始曲率的变化量分别为:
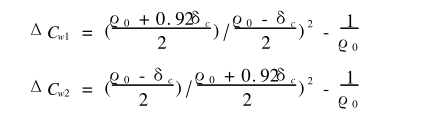
5)总变形曲率变化量(1/mm)。
ΔC=ΔC0+ΔCW
上式为原始曲率与反弯曲率变化量之代数和,计算时需要区别两者正反方向。
6)残余曲率变化量。
ΔCC=ΔC-ΔCy
式中ΔCy为弹复曲率变化量,1/mm。
7)残余椭圆度(1/mm)残余曲率变化量为:
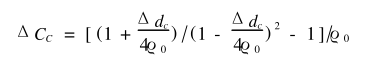
根据上式化简后得矫正后的残余椭圆度:
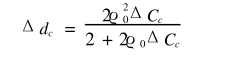
8)矫正次数[5]。
设矫正辊的长度为L,矫正钢管时旋转导程为:S=/dtanα,则每对辊压扁矫正次数:i=4L/S。
2钢管矫正过程研究
2.1理论分析
根据以上钢管圆度矫正变形理论对2-2-2型○/168钢管矫正机的矫正过程进行了分析,计算程序如图2所示。
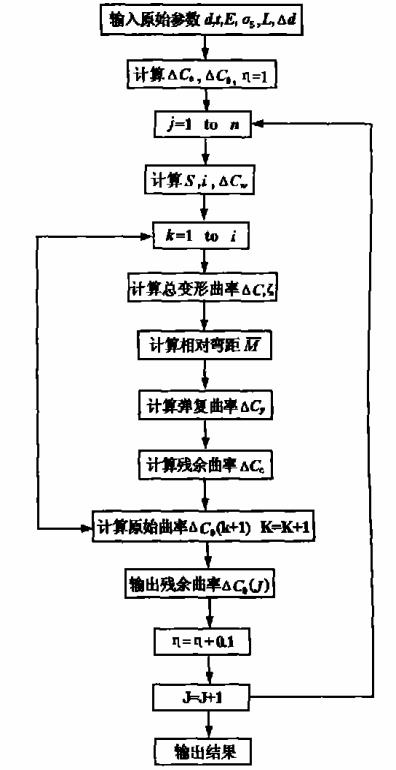
图2 残余曲率计算程序
矫正机的基本参数:长度L=260mm,角度α=28°,矫正范围○/50~168mm。本文从3个方面进行分析。
1) 3种不同规格的管材矫正过程研究:力学性能指标为σs=400MPa,尺寸规格①d=50mm,t=5mm,Δd=1mm;②d=76mm,Δd=1.5mm,t=6mm;③d=140mm,Δd=2.5mm,t=6.5mm。由于原始曲率变化量在长短轴位置不同,分析时仅以其中一个曲率的变化进行分析。设3对矫正辊的压扁量相同,则完全矫正后的相对残余曲率与压下设定值之间的关系如图3所示。
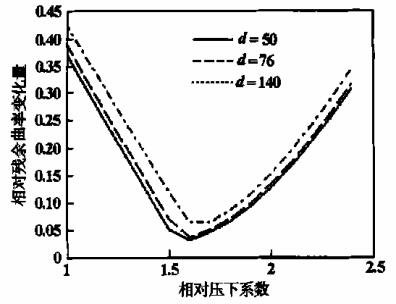
图3 相对压下系数与相对残余曲率的关系
1号~3号轧件的最小相对残余曲率:0.0312,0.0359,0.0638。相对压下系数:1.6,1.6,1.7。
2) 3种不同钢种矫正过程研究:尺寸规格:d=76mm,Δd=1.5mm,t=6mm钢管屈服强度①σs=400MPa;②σs=325MPa;③σs=245MPa。
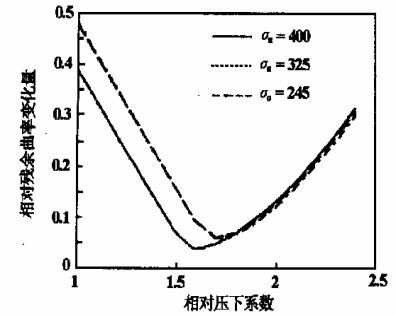
图4 相对压下系数与相对残余曲率的关系
最小相对残余曲率:Cc1=0.0359,Cc2=0.0611,Cc3=0.0585。相对压下系数:η1=1.6,η2=1.7,η3=1.7。
3) 单件产品在3对矫正辊矫正时设定不同压扁量的矫正过程分析:以○/76mm,σs=400MPa管材为例说明1号矫正辊矫正过程相对残余曲率变化。
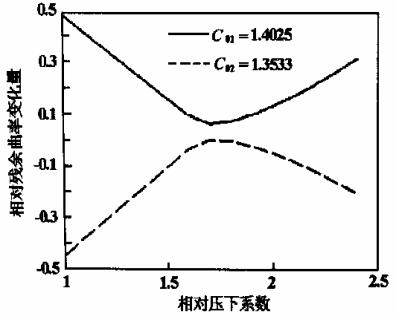
图5 相对压下系数与相对残余曲率的关系
长短轴相对原始曲率:C01=1.4025,C02=-1.3533,最小相对残余曲率Cc1=0.0635,Cc2=-0.0013。相对压下系数:η1=1.7,η2=1.8。
2号矫正辊矫正过程相对残余曲率变化见图6。
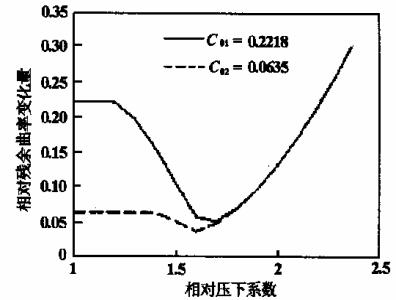
图6 相对压下系数与相对残余曲率的关系
相对原始曲率C01=0.2218(1号辊η=1.4),C02=0.0635(1号辊η=1.7)。最小相对残余曲率Cc1=0.0531,Cc2=0.0388,对应的相对压下系数η1=1.7,η2=1.6。
3号矫正辊矫正过程相对残余曲率变化见图7。

图7 相对压下系数与相对残余曲率的关系
最小相对残余曲率Cc1=0.0373,Cc2=0.0352。相对压下系数η1=1.6,η2=1.6。
2.2实际残余椭圆度
以某厂2-2-2钢管矫正机组为例,在原始椭圆度基本相同(Δd≈1.7mm)的条件下,设定不同矫正压扁量时获得的残余椭圆度(产品规格:○/60,t=5,σs=245MPa)如表1所示。
表1设定不同矫正压扁量时获得的残余椭圆度
3分析
1)通过对过程的计算分析基本揭示钢管矫正过程残余圆度的变化规律。由图3、图4可知,对22222型矫正机,在矫正辊参数一定条件下,压扁量的设定将决定矫正机的矫正效果。3种不同规格、材质的钢管在3对辊同一压扁量作用下矫正时相对残余曲率与相对压下系数的关系,曲线存在最小极值点,对应的相对压下系数均在1.7左右。由此说明对同种材质的管材在矫正时实际压扁量设定在1.6~1.8倍弹性极限压扁量时效果最为理想。根据残余圆度计算公式得钢管的残余椭圆度分别为:Δdc1=0.0168mm,Δdc2=0.0391mm,Δdc3=0.2328mm。可见残余椭圆度远远小于允许值。另外由相对残余曲率与相对压下系数的关系表明最佳压扁量与弹性极限压扁量相关,即不仅与被矫钢管直径有关,而且与屈服强度、管材壁厚有关。
2)单一产品在每对矫正辊上的矫正时相对残余曲率变化过程如图5~图7所示。由1号矫正辊上的矫正过程显示,矫正前管材长短轴的原始曲率在矫正后均存在最小残余曲率区间,与图2所示规律相同,相对压下系数为1.6~1.8。对2号矫正辊在矫正时,如果原始椭圆度按前辊的最小残余曲率确定,则相对压下系数在小于1.5范围内对原始曲率没有矫正效果,仅在1.6~1.7附近有少量改进。如果原始椭圆度按前辊的非最小残余曲率确定,则1号辊矫正后的残余曲率在2号辊矫正时仍有较大改进,其最小残余曲率极值点仍在η=1.6~1.7范围内。在3号辊矫正时,取最小残余曲率作为原始曲率,则相对压下系数在1.6以下对矫正效果几乎没有影响。当η=1.6时,最小残余曲率基本相等。当η超过1.6时残余曲率将不断增加。说明对22222型矫正机,设定压扁量时只要基于最优选择时,则矫正过程完全可以在1~2号矫正辊上实现,3号矫正辊仅起精整作用。
3)由残余椭圆度实测可知,产品的实际压扁量与残余椭圆度的对应关系与理论分析结果基本相一致,存在一个最优范围。
4结语
以上基于弹塑性理论的研究与比较基本说明了不同规格、不同钢种的钢管圆度矫正过程的变化规律。压扁量设定值如果过小压扁效果不明显,设定值过大反而使残余椭圆度增大。压扁量的选择存在一个最佳区间,即η=1.6~1.8。因此合理选择压扁量就可以使管材的残余椭圆度明显减少,钢管的圆度精度显著提高。为今后更合理地制定矫正工艺提供了理论基础,对提高矫正质量具有一定的实际指导意义。
参考文献
[1]宋华.斜辊钢管矫正机压扁量的确定.钢管,1999(3):10~14
[2]梁炳文.弹塑性稳定理论.北京:国防工业出版社,1983
[3]朱美珍.对向六斜辊管材矫直机压扁压下量研究.包头钢铁学院学报,1998(1):33~35
[4]崔甫.矫直理论与参数计算.北京:机械工业出版社,1994
[5]李德惠.六辊矫直机的技术特性.钢管,1991(1):20~24