钢管材料的洛氏硬度与抗拉强度的关系

我们在从事相关试验工作中发现：钢管材料金属硬度越高，材料强度越大，为了找出洛氏硬度和拉伸强度这两个变量在一定范围内存在的关系，我们选取16组石油钻杆管体试样，通过机加工分别制备成拉伸试样与洛氏硬度试样，并进行拉伸试验和洛氏硬度试验。

试样制备与试验方法

1.洛氏硬度试样的制备

图1 洛氏硬度试样宏观形貌

按GB/T 230.1-2018«金属材料洛氏硬度试验第1部分：试验方法»规定进行制备，洛氏硬度试样如图1所示。

2.洛氏硬度试验方法

依据GB/T 230.1-2018，试验在室温下(10~35℃)进行，因为温度的变化可能会对试验结果有影响。试验台应平稳地放在刚性支承物上，表面不得有铁屑及其他脏物，并使压头轴线与试样表面垂直，避免产生位移。使压头与试样表面接触，无冲击和振动下均匀地施加初始试验力F0，初始试验力保持时间不应超过3s，从初始试验力F0施加至总试验力F的时间应不小于1s且不大于8s。总试验力F保持时间为(4±2)s。然后卸除主试验力F1，保持初始试验力F0，经过短时间稳定后，读数并记录，每组测试16点洛氏硬度，取平均值，试验结果见表1。

3.拉伸试样的制备

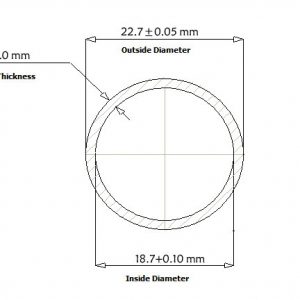
按GB/T 228.1-2010«金属材料拉伸试验第1部分：室温试验方法»中附录E规定制成全壁厚纵向矩形试样，如图2所示。

图2 拉伸试样宏观形貌

4.拉伸试验方法

所用拉伸试验机型号为WHW-600，引伸计型号为FS-004，级别为0.5级，标距为50mm，试验控制软件为RE_TEST 版2.0 Copyright(C)2006，试验温度为(23±5)℃。试验时确保被夹持试样受轴向拉力的作用，避免斜拉，斜拉有可能使被测试样受力不均匀，从而影响试验结果的准确性。试验速度控制模式为位移控制，横梁位移速度为1.5mm·min-1，拉伸试验结果见表1。

表1 拉伸和洛氏硬度试验结果

试验结果分析

1.散布图

为了研究洛氏硬度与抗拉强度之间的关系，根据试验数据画出散布图，横坐标为洛氏硬度，纵坐标为对应的抗拉强度，如图3所示。

图3 洛氏硬度与抗拉强度的散布图

由图3可知，当材料的洛氏硬度增加时，其抗拉强度也呈上升趋势。因此，可用回归分析法来分析洛氏硬度与拉伸强度之间的关系。

2.相关系数

由图3可知，16个测试点基本在一条直线附近，但又不完全在一条直线上，为了表示洛氏硬度与抗拉强度之间线性关系的密切程度，用统计量r来表示两个变量的相关系数

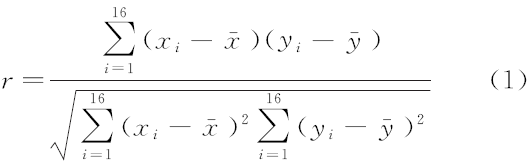
式中：x表示洛氏硬度，y表示抗拉强度。

r>0，表示两个变量正相关，即x越大y就有增大的趋势；r<0，表示两个变量负相关，即x越大y就有减小的趋势；r=0，表示两个变量不相关，但是有可能存在某种特殊的曲线关系。由于相关系数是根据样本求出来的，即使两个变量不相关，但是求出来的相关系数也不一定恰好等于0。

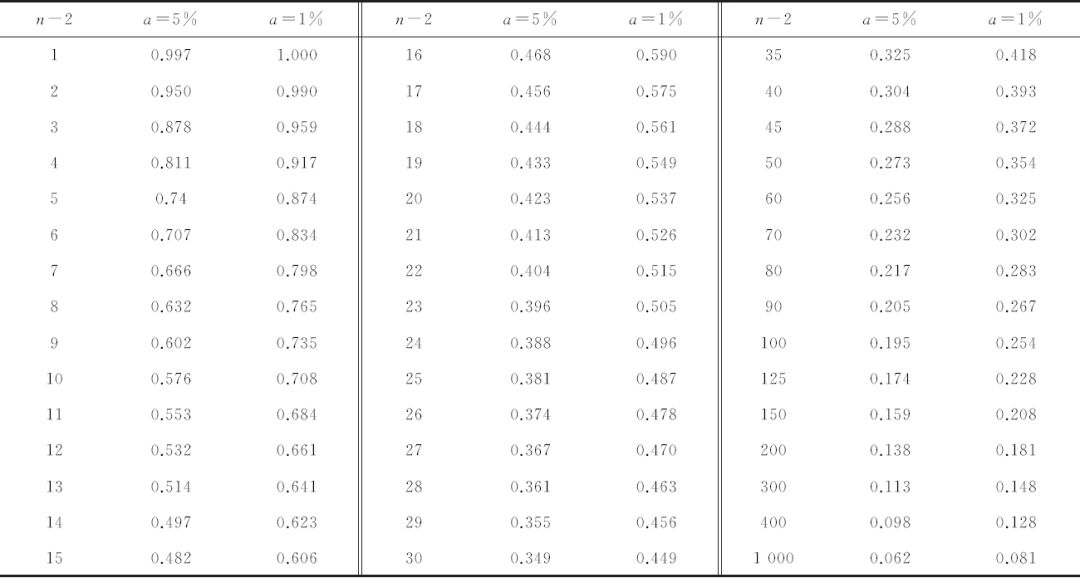
3.相关系数的检验

经过计算可得r=0.78。查阅表2检验相关系数的临界值，由于计算得出的r>0.497，即试验计算得到的数据落在拒绝域区域， 洛氏硬度与抗拉强度存在正线性相关关系。

表2 检验相关系数的临界值表

洛氏硬度与抗拉强度的一元线性回归方程

经过计算后课求得的一元线性回归方程为：y =496.55+14.704x (2)

一元线性回归方程的显著性检验

建立回归方程的目的，是为了将两个具有线性关系的变量用公式表达出来，由于数据来源于试验，试验中不可避免地会产生误差。可以通过统计技术方法如方差分析对所求得的方程进行显著性检验，即检验所求得的方程是否有意义。

试验中造成数据波动的原因有两个：一个是由于自变量x的取值不同，得到不同的y值；另一个是除了自变量x以外的一切因素，统称为随机误差。

经计算， a=0.05水平上回归方程是显著的。

利用回归方程进行预测

当洛氏硬度值为28.1时，能有置信度为95%概率的把握，预测抗拉强度为852.92~966.54MPa，预测区间示意图如图4所示。

图4 预测区间图

由图4可知，当x0越靠近时，区间宽度越窄，预测的精度越高。

文中样本空间n仅取16，所取硬度范围为21~30HRC，实际中的抗拉强度与洛氏硬度之间的回归问题应取足够的样本空间，从而建立起回归关系式。

结论

(1)任何强度､硬度换算表都不可能详细给出任意硬度､抗拉强度的换算值，所以对大量试验数据进行计算机回归处理，得到拉伸强度与洛氏硬度之间的回归关系是有实际意义的。

(2)洛氏硬度与抗拉强度之间不应是直线关系而应是曲线关系，但在一定范围内可以近似看作线性关系。

(3)所得到的回归关系式为y=496.55+14.704x，在生产条件固定的情况下，洛氏硬度检测快速､简便，对于某些不能进行拉伸试验也不便进行布氏硬度试样和仪器压痕试验的材料，可以通过预先得到的回归方程估算其抗拉强度。

钢管材料万能拉伸试验机