大口径钢管圆度测量喷标系统设计与误差补偿研究
为满足大口径钢管测量精度的需要,设计了一种龙门架式钢管在线测量及喷标系统。利用龙门架两侧立柱激光传感器的竖直运动,测量钢管截面外径上点的坐标,利用最小二乘法求其圆心坐标,采用近似直径法求取该截面的最大直径和最小直径,从而求得该截面的圆度。实例证明该系统及数据处理算法可实现钢管外径及圆度的测量,并具有相当高的精度。对测量结果进行误差分析,得知影响测量结果的主要来源是钢管的摆放姿态,通过投影及坐标变换对误差进行补偿,补偿后结果得到了一定的改善,从而验证了误差分析的合理性和补偿方法的可行性,该系统可用于大口径钢管的在线测量。
引言
为了满足恶劣环境下钢管对接及装配的需求,必须对钢管的质量提出更高的要求[1~2]。钢管检测主要分为探伤检测和外形检测,外形检测主要包括对长度、端面垂直度、直径、圆度、壁厚、直线度等参数的测量,大型企业对钢管生产及检测时还需进行相应的喷标处理。
钢管圆度测量的方法主要分为接触式测量和非接触式测量。接触式测量常采用长脚卡尺和圆度仪,有三点法[3]、两步法[4]、多步法[5]等,但只适合于小直径管,且效率低、受人为因素影响较大,不适合大规模及大直径管的在线测量;随着光电设备的迅速发展,非接触式测量[6]逐渐得到应用,肖鹏[7]等采用CCD技术进行动态测量,王宏[8]等基于Labview平台采用三点法进行测量,姜晓勇[9]等提出MWS系统进行在线测量,黄富贵[10]等用谐波分析法识别圆度误差特征,但上述方法在测量精度及综合测量功能上都有待提高。
本文提出一种在线钢管检测系统,针对圆度误差,采用两个伺服电机通过丝杠传动分别控制两个激光传感器作竖直方向运动,激光传感器水平测量钢管表面的点,从而得到这些点水平坐标和垂直坐标,通过近似计算获得圆度值。本文对在线测量的某钢管外径数据进行计算,并分析测量时误差产生的机理,对所测数据进行补偿。
1钢管测量及喷标系统
1.1系统结构
钢管测量及喷标系统采用如图1、2所示的龙门架式结构,龙门架由两侧的伺服电机通过减速器驱动,可沿导轨水平移动;龙门架顶部横梁上装有导轨,顶部测量臂和喷标臂分别位于横梁两侧,由伺服电机通过丝杠控制,可在横梁上移动;测量臂和喷标臂均安装有伺服电机和丝杠,从而可以在竖直方向运动,测量臂下端两侧水平装有两个激光位移传感器,用于端面垂直度和钢管长度的测量,底部装有测厚仪,用于测量钢管的壁厚,喷标臂下端装有喷头,用于钢管喷标;龙门架两侧立柱装有直线导轨和伺服电机,两个导轨均水平装有激光位移传感器,用于钢管直径及圆度测量;地面导轨的一端装有激光位移传感器,用于龙门架位置和钢管长度的测量。
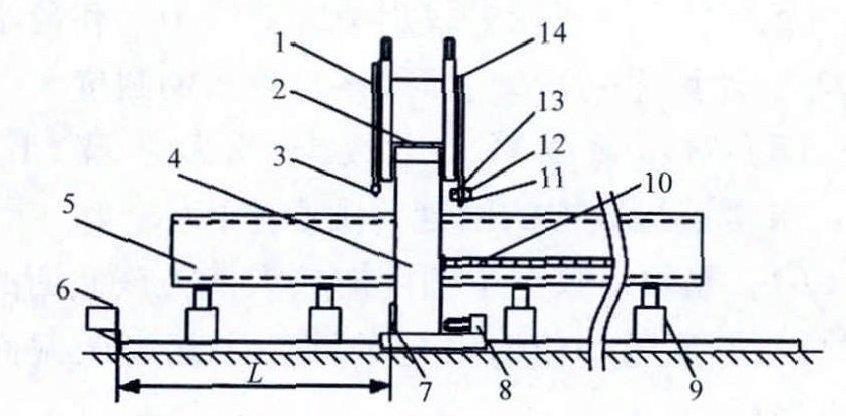
图1钢管测量及喷标系统主视图
1.喷标臂,2.横梁导轨,3.喷头,4.龙门架,5.钢管,6.激光传感器1,7.反光板,8.电机、减速机,9.辊道,10.坦克链,11.测厚仪,12.激光传感器2,13.激光传感器3,14.测量臂
整个系统由工控机控制,测量前只需将龙门架停到钢管左侧,设置好参数后整个测量及喷标过程中无需操作,测量时间随测量截面数的不同而变化,以测量3个截面为例,大约需要10min。该系统设有各种限位及故障保护,安全可靠。
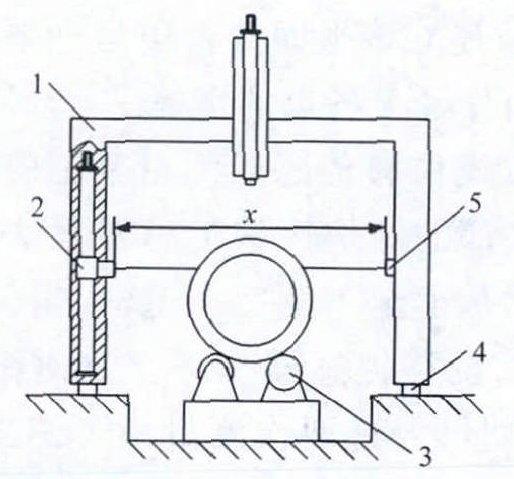
图2钢管测量及喷标系统侧视图
1.龙门架,2.激光传感器4,3.辊道,4.导轨,5.激光传感器5
1.2圆度测量原理
测量时钢管放置于支撑辊道上,每个辊道上有两个伺服电机,可使钢管转动以及水平方向移动,测量过程中钢管保持静止状态。
圆度测量如图1、2所示,龙门架停至钢管某待测截面位置,激光传感器1测得龙门架位置L。测量前需将龙门架两侧支柱的激光传感器4和5调至同一高度,该系统中龙门架两立柱导轨中激光传感器的起始位置各装有一个限位开关,安装时通过重锤和直尺保证两限位开关在同一高度,测量时先检测两传感器是否到达限位,如未到达限位则先将传感器移至限位开关位置,同时通过设置两侧立柱伺服电机速度使两传感器移动速度相同,从而使其制动距离相同,进一步保证两侧传感器在同一高度处开始检测。
圆度测量前还需测出两传感器端面间的距离x,具体测法如图3所示,本系统中选用l=1m长标准量块水平置于两传感器中间,两侧传感器分别测出到量块的距离x1、x2,则x=x1+l+x2。两传感器端面距离只需定期进行标定即可,其精度取决于传感器精度以及量块的水平精度,可通过多次平均提高精度,由于该误差精度远小于圆度误差,因而对后续的数据处理影响很小。
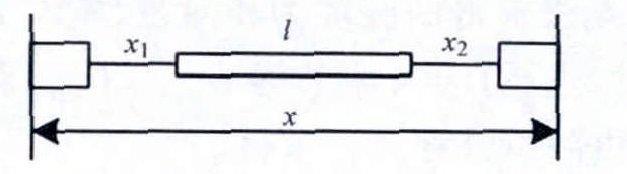
图3传感器端面距离测量原理图
激光位移传感器在伺服电机的驱动下竖直向下运动,传感器的竖直位置可由伺服电机编码器的反馈脉冲计算获得,传感器下降过程中依次测得钢管外径各点的水平位置,当电机速度足够慢或采样频率足够高时,理论上可以测得外径上整个测量范围内轮廓上所有点的位置。
取两传感器初始最高位的中点为该截面的坐标原点,竖直向下方向为y轴正方向,水平向右方向为x轴正方向,建立该平面的直角坐标系,从而可以得到所测截面外径上各点的坐标。
由于激光位移传感器测量范围的限制,钢管接近顶部和底部的两块区域传感器无法测到,因而当位移传感器从上至下测完一遍时,需转动辊道使钢管旋转90°,位移传感器从下至上对钢管该截面再进行一次测量,经过两次测量便可测出该截面各个位置点的坐标,对两组数据分别进行圆度求解,取结果较大值为该截面圆度。
本系统采用LK-G500型高精度激光位移传感器,测量范围250~1000mm,重复精度0.002mm,光点小且适合小角度测量。经测量两传感器端面距离为1966.65mm,考虑到传感器量程以及适合测量的角度范围,并且考虑到每次采样点应覆盖圆周至少2/3的范围,本系统可测量的钢管外径范围为200~1400mm,因而本系统可用来测量大口径钢管,同时也适用于小口径钢管。
为了得到直线度,需对钢管至少3个截面进行测量。设空间坐标系z的正方向沿导轨水平向右,z轴零点在激光传感器1的端面位置,经圆度计算可得每个截面的圆心坐标,由3个以上的圆心坐标即可获得钢管的直线度。
2圆度计算
2.1圆度定义
圆形钢管的横截面上存在着外径不相等的现象,即存在着不一定互相垂直的最大外径和最小外径,则最大外径与最小外径之差即为不圆度(或椭圆度),钢管圆度公式为[11]

这种方法求得的圆度为相对量,本文只针对圆度的绝对量进行计算,即求解Dmax-Dmin,圆度误差的相对量可除以公称直径求得。
2.2圆度求解
根据定义,若求解钢管某截面圆度,只需找出该截面的最大直径和最小直径。本系统采用近似直径测量方法,用激光传感器测量钢管某截面外径上大量点的坐标,如图4所示,Ai表示左侧传感器采集到钢管外径左半部分点的坐标,Bj表示右侧传感器采集到钢管外径右半部分点的坐标,伺服电机转速越慢,采样频率越高,则采集到的点越密集,测量结果越精确。
对采集到的点进行处理,步骤如下:

图4圆度测量及求解示意图
(1)根据该截面的第1组数据,求解该截面最小二乘圆心坐标(xO,yO)。
(2)比较左右两侧采样点数目,以采样点少的一侧为基准,图4中以左侧点为基准点,以下均以此情况为例。
(3)对左侧每个点分别进行计算,以第i个点计算为例:第i个点Ai的坐标为(xAi,yAi),找出右侧点坐标中与其可能构成直径的点Bj(xBj,yBj),所找
的点需满足
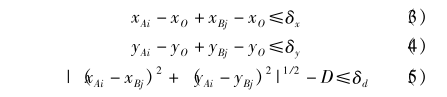
式中δx、δy、δd分别为横坐标、纵坐标及直径的偏差,为计算准确,可选允许的圆度绝对误差的2倍,如果某点处未找到对应点,则需将偏差适当放大再计算。
(4)假设对于左侧点Ai,找得右侧点Bj满足以上条件,分别求出Bj前后各两点和Ai的距离,取最大值作为Ai点处的直径,若Bj前后某一侧少于两点,则在另一侧多加相应点数进行计算。
(5)在所得直径中找出最大直径Dmax和最小直径Dmin,计算Dmax-Dmin即得该组数据的圆度。
(6)对该截面第2组数据,重复步骤(1)~(5),求得该组数据的圆度和圆心坐标。
(7)取两组数据中圆度的较大值为该截面的圆度值,取圆度较小值时对应的圆心坐标为该截面的圆心坐标。
2.3计算方法实例分析
实际测量前,运用该系统对管径500mm、长度1000mm、圆度误差为0.50mm的标准管的一个截面进行多次测量,测得圆度误差在0.47~0.54mm之间,因而该系统具有很高的精度,系统如图5所示。

图5钢管测量系统
对某公称直径为637mm、长度为5700mm的未经精加工的钢管进行测量,测量3次,测量截面与激光传感器1的距离L分别为2560mm、3954mm、5473mm,测量结果如图6所示。

图6 3个截面的外径测量结果
图6a为每个截面第1次测量结果,图6b为钢管旋转90°后的测量结果,钢管顶端和底端各有一片区域未能采集到。
经计算,各截面圆心坐标、直径及圆度的绝对量分别如表1所示。
表1各截面测量结果
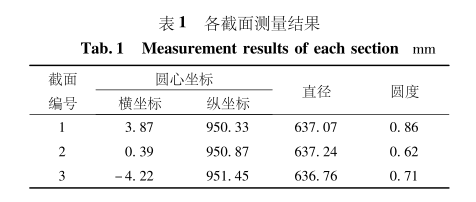
从计算结果可知,考虑到钢管未经过精加工,所测结果已具有很高的精度,但所得圆度偏大。现场测量时对钢管进行粗略检查,并未发现钢管表面有明显的凸起和凹陷,因而测量结果存在一定的误差。
3误差分析及补偿
3.1误差产生机理
与以往钢管测量系统相比,本测量系统的最大优点在于激光传感器由丝杠传动竖直运动以及测量时钢管处于静止状态。由于测量过程中钢管无需转动,因而数据处理时无需考虑钢管运动时振动带来的影响,又由于丝杠传动具有精度高、运动平稳的特点,因而激光传感器运动过程中产生的振动基本可以忽略。此外激光传感器采用串口通讯,避免了模拟量通讯时信号衰减带来的影响,保障了信号传输精度。
经过分析,本系统的误差主要存在于以下几个方面:安装精度、测量精度、辊道旋转精度、环境干扰及钢管摆放位置精度。
安装精度包括龙门架两立柱丝杠的垂直度、两侧激光传感器的起始高度、传感器激光束与丝杠的垂直度以及两侧激光束是否位于同一平面,这些因素均可以通过机械调整使其控制在一定范围内。
测量精度包括两激光传感器端面距离的测量精度以及传感器本身的测量精度,前者可以控制,后者需根据测量精度合理选择。
辊道旋转精度主要是指对钢管某截面进行测量时,钢管顶部和底部部分区域存在测量盲区,为了避免由此造成的误差,需要对该截面进行两次测量,两次测量中间需要转动辊道使钢管旋转90°,由于辊道底盘可以旋转(为了能够驱动钢管自转以及前后移动),因而辊道转子的主轴方向与钢管轴线方向可能存在夹角,导致辊道转动时钢管除了自转还会前后移动,使得第2次测量的点与第1次测量的点不在同一截面,从而带来误差。解决方法:在辊道底座边缘加装接近开关进行控制,使辊道转子轴线与钢管轴线尽量平行;使二者轴线形成一定夹角,测量前先转动辊道,测出钢管移动的距离,测量时钢管转动后龙门架移动相应位置进行补偿。但二者都无法完全消除误差。
环境干扰是指同一车间其它生产加工设备工作时产生的振动对测量造成的影响。该系统地基四周与厂房地面通过1.5~2m的深沟隔开,同时该生产线附近不设置大型加工设备,一定程度上可以减少环境对测量的影响。
影响圆度误差的最大因素在于钢管的摆放精度,如图7所示,由于辊道固定位置、高度以及支撑辊存在位置偏差,使得钢管轴线与系统测量截面(两侧激光传感器激光束所在的平面)不垂直,钢管实际轴线与系统z轴存在α的偏角。
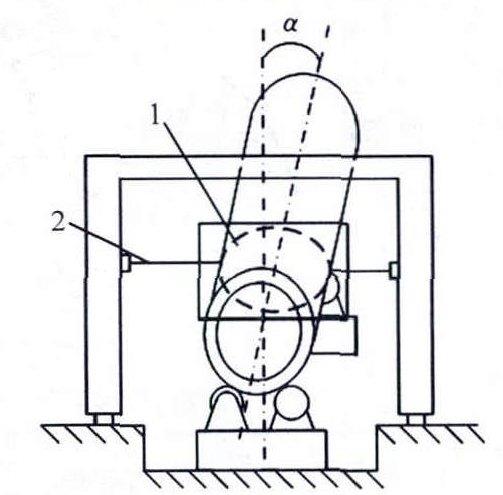
图7钢管实际摆放姿态示意图
为了验证这一点,将上例中钢管被测3个截面的圆心投影到同一个坐标系,结果如图8所示,可以看出3个圆心并不重合,且呈现出一定的线性关系,若将3圆心沿z轴延伸至所测截面各位置处,可知钢管轴线必然与z轴存在偏差。
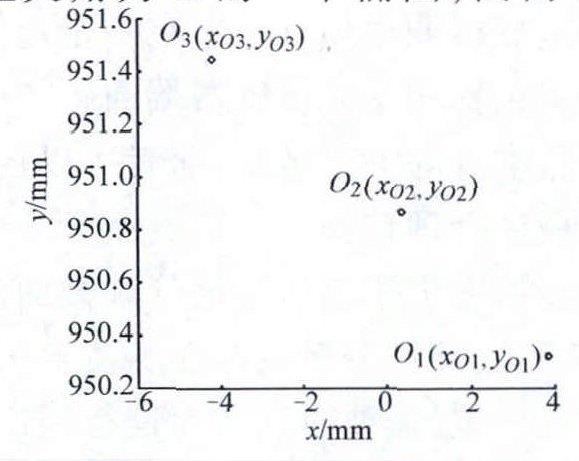
图8不同截面圆心坐标
由于钢管摆放位置存在倾斜,实际测到的截面并非是垂直于钢管轴线的截面,而是与该截面同圆心且夹角为α的一个椭圆,因而计算得到的圆度必然存在着一定的误差,此误差需经过计算进行补偿。
3.2圆度误差补偿
为了获得与钢管轴线垂直截面的圆度,需要对所测点进行补偿,补偿方法是求出过该测量面圆心且与轴线垂直的截面位置,将所测点投影到该截面上,进而进行计算。
如图9所示,A1是测量截面,O1是测量得到的点,A2是所要投影的截面,O2是投影后的点,l是两个面的交线,O(xOi,yOi)为公共圆心。误差补偿的
步骤如下:

图9测量面与实际截面位置关系
1)根据不同测量截面的圆心坐标,用最小二乘法拟合出圆心所在直线的方向向量L(l,m,n),即各投影截面的法向量,进而求出L与z轴正方向的夹角α=〈(l,m,n),(0,0,1)〉。
(2)对于某一测量截面A1,将所测得的点的坐标(x1i,y1i,z1i)投影到A2上,得到其投影后的坐标(x2i,y2i,z2i),其中z1i为该截面到激光传感器1的距离。
(3)坐标变换[12]:将空间坐标系原点移至圆心O处,平移矩阵为

将所得坐标系沿新的z轴旋转θ,旋转矩阵为

式中θ求解方法为:如图10所示,θ1为L与平面A1的夹角,由图知θ1=π/2-α,θ2为L与x轴正方向的夹角,θ2=〈(l,m,n),(1,0,0)〉,由几何关系可知

需注意θ的符号,当L在xy平面内的投影在一、三象限时取正值,在二、四象限时取负值,最后将θ值取反后代入到式(7)中。

图10 θ角求解示意图
再将坐标系绕y轴旋转-α,即得到A2平面内的坐标系,转换矩阵为
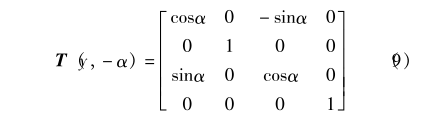
4)将A2上点的原始坐标转换为A2平面内坐标系的坐标,为了使转换后的左侧点和右侧点坐标对称,将转换后的坐标再绕新的z轴旋转-θ,变换公式为

对2.3节中的3个截面点坐标变换后舍去z向坐标,所得结果如图11所示。
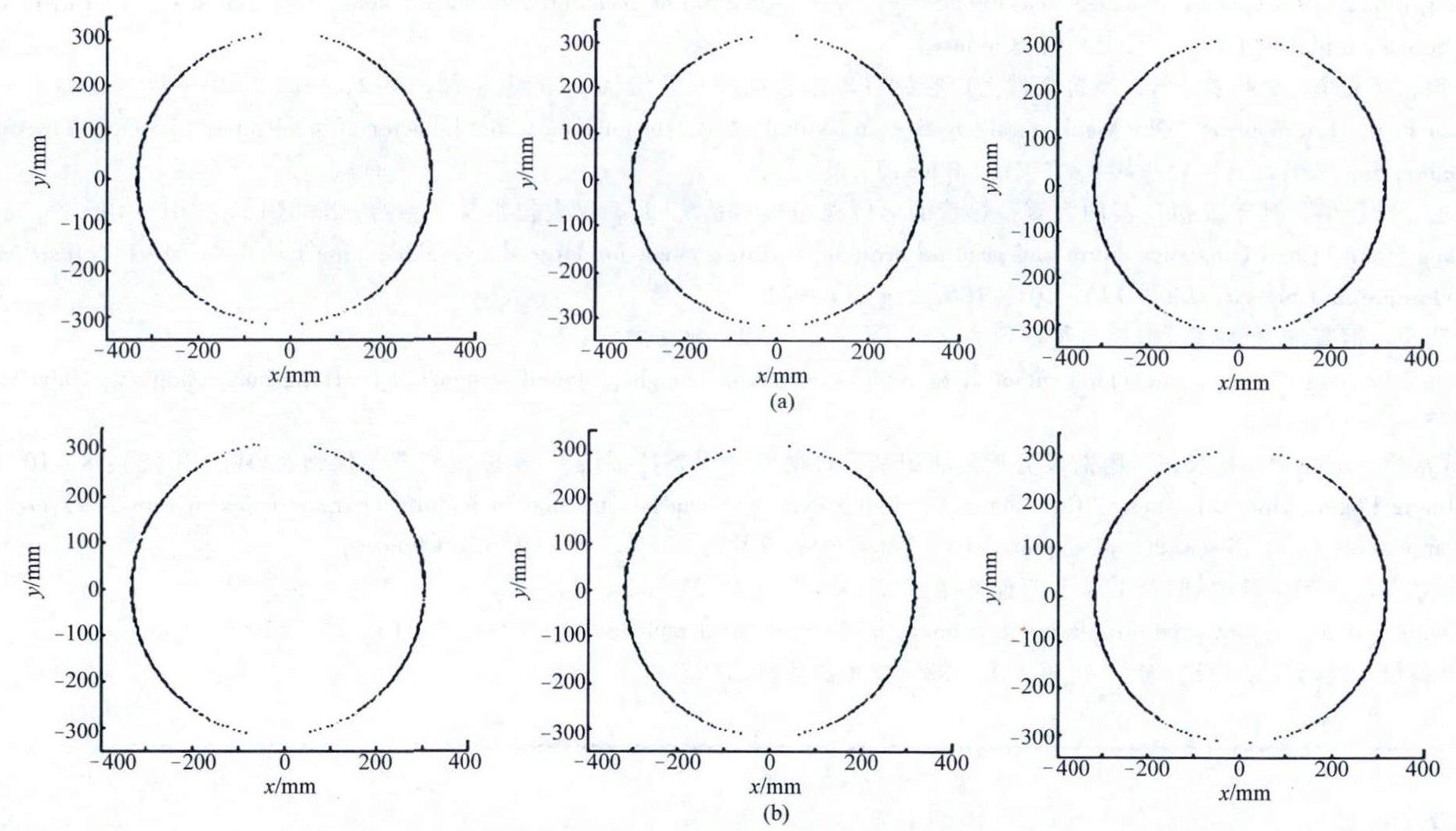
图11误差补偿后3个截面外径测量结果
对坐标变换后的点按2.2节所述方法计算圆度,变换后的圆度如表2所示。
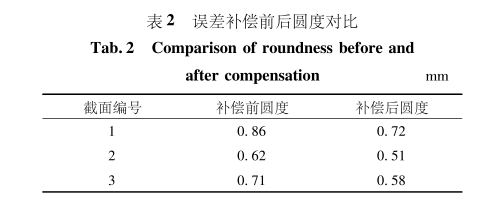
由表2可知,补偿后圆度值得到改善,更接近实际值,说明用本文的方法进行补偿行之有效。
4结束语
提出了一种用于大口径钢管测量的新方法。利用龙门架两侧立柱激光传感器的竖直运动,测量钢管截面外径上的点的坐标。本方法测量过程中钢管无需转动,仅在每个截面两次测量的间隔转动钢管,消除了钢管运动过程中振动带来的误差。对采集到的数据点通过近似直径计算得到截面的最大直径和最小直径,进而算得该截面的圆度。针对圆度偏大的现象,对误差机理了进行分析,得出误差主要来源在于钢管摆放位置与测量截面不垂直,经过补偿,将测量截面的点投影到实际直径截面,再次计算圆度,计算结果得到改善,从而验证了误差分析的合理性和补偿算法的可行性。该系统及测量方法可用于大口径钢管的圆度测量,并且由于控制简单、算法简便、测量时间短,适合于工厂对钢管进行大批量的在线测量。
参考文献
1. 周锦进,阿达依·谢尔亚孜旦,安晓刚.电化学机械加工在碳钢管内孔光整中的应用[J].农业机械学报,2005,36(10):145~148.ZhouJinjin,AdayiXieeryazidan,AnXiaogang.ResearchandapplicationofECMMininnersurfacefinishing[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2005,36(10):145~148.(inChiense)
2. 胡龙飞,刘全坤,王成勇,等.基于多目标优化的钢管拉拔成形过程设计[J].农业机械学报,2007,38(10):161~164.HuLongfei,LiuQuankun,WangChengyong,etal.Formingprocessdesignofpipedrawingbasedonmulti-objectiveoptimization[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2007,38(10):161~164.(inChinese)
3. MuralikrishnanB,VenkatachalamS.Anoteonthree-pointmethodforroundnessmeasurement[J].PrecisionEngineering,2005,29(3):257.
4. 赵维谦,谭久彬,杨文国,等.基于两步法超精密圆度仪误差分离系统[J].中国机械工程,2000,11(11):1206~1208.ZhaoWeiqian,TanJiubin,YangWenguo,etal.Ultra-precisionroundnesserrorseparationsystembasedonthetwo-step separationmethod[J].ChinaMechanicalEngineering,2000,11(11):1206~1208.(inChinese)
5. 赵维谦,谭久彬,常承,等.超精圆度仅全自动误差分离装置的研制[J].仪器仪表学报,2000,21(2):203~205.ZhaoWeiqian,TanJiubin,ChangCheng,etal.Developmentofautomaticerrorseparationsystemforultra-precisionroundnessinstrument[J].ChinaJournalofScientificInstrument,2000,21(2):203~205.(inChinese)
6. 姜丽华.非接触式实时在线线径测量系统的研究与开发[D].大连:大连理工大学,2005.JiangLihua.Non-contactdiametermeasurementsystemreal-timeonlineresearchanddevelopment[D].Dalian:DalianUniversityofScienceandTechnology,2005.(inChinese)
7. 肖鹏,刘文耀,裘稀石,等.高抗振性大口径钢管动态直径测量系统[J].光电工程,2012,39(1):40~47.XiaoPeng,LiuWenyao,QiuXishi,etal.Activeanti-vibrationsystemformeasuringdiameterofsteelpipe[J].Opto-ElectronicEngineering,2012,39(1):40~47.(inChinese)
8. 王宏,陈庆峰.基于虚拟仪器的大直径焊管的形位误差检测系统[J].仪表技术与传感器,2008(12):101~106.WangHong,ChenQingfeng.Formandpositionerrormeasuringsystemforlargedia.weldedpipebasedonⅥ[J].InstrumentTechniqueandSensor,2008(12):101~106.(inChinese)
9. 姜晓勇.钢管测量、称重、喷标系统的研究与开发[D].杭州:浙江大学,2003.JiangXiaoyong.Study&developmentofsteeltube’smeasure,weight,stencilsystem[D].Hangzhou:ZhejiangUniversity,2003.(inChinese)
10. 黄富贵,董兆鹏,崔长彩.用谐波分析方法识别零件的圆度误差特征[J].实验室研究与探索,2011,30(8):8~10.HuangFugui,DongZhaopeng,CuiChangcai.Usingharmonicanalysismethodtoidentifycharacteristicsofroundnesserrorofcomponents[J].ResearchandExplorationinLaboratory,2011,30(8):8~10.(inChinese)
11. 张复兴.关于钢管的圆度[J].上海计量测试,2004,31(1):21~22.ZhangFuxing.Aboutpipecircularity[J].ShanghaiMeasurementandTesting,2004,31(1):21~22.(inChinese)
12. 蒋新松.机器人学导论[M].沈阳:辽宁科学技术出版社,1993.
全文PDF格式下载: