本文针对大直径钢管截面的圆度测量在多数企业中仍采用人工作业的不足,为提高工作效率及降低人工成本,设计了一套大口径钢管圆度测量系统.该系统以工业机器人作为载体,利用高精度激光位移传感器实现对大口径钢管截面圆度的非接触式测量,同时为解决激光位移传感器沿钢管轴线平行方向测量的问题提出机器人测量姿态调整方案.针对传统方法求解圆度误差较为困难及评定精度不高的问题,提出将鲸鱼优化算法应用于圆度误差评定,根据最小区域原则建立鲸鱼优化算法得到目标函数,并论述了该圆度误差评定的原理及步骤.试验结果表明,该系统的测量方法能够实现钢管的圆度测量,同时也验证了鲸鱼优化算法在圆度误差评定中的有效性.
随着我国钢管的需求量不断增加[1],对钢管的生产质量也提出了更高的要求,而钢管截面的圆度误差是否合格是把关钢管生产质量的重要指标.在目前多数生产企业中,对于钢管截面的圆度误差测量多是人工采用千分尺、百分表、圆度仪进行测量,人工测量时通常带有人为因素成分以及所采用的是接触式测量方法,这不仅使得测量精度低下,而且更影响测量效率.为了提高测量效率和降低人工成本,各企业急需一种能采用工业自动化的测量设备来代替人工测量.目前国内外已有一些测量设备,如三坐标测量机等,但这些设备普遍费用昂贵,同时在复杂的工业现场中也较难去应用.为解决上述问题,提出一种采用工业机器人携带激光位移传感器对钢管截面圆度进行非接触式自动化测量的方法,并对其进行实验验证,该测量系统简单实用,重复精度和稳定性都能较好地满足实际需求。
圆度误差评定的计算问题其本质上是非线性优化问题,传统的计算方法对其求解较为困难,而智能算法对于求解非线性优化问题较为方便.目前将智能算法应用于圆度误差评定中较多,王宸[2]等提出将改进天牛须搜索算法应用于圆度误差评定中,提高了圆度误差评定精度;罗钧[3]等将改进的蜂群算法应用于圆度评定中,并取得了较好的结果;崔星星[4]等提出将改进后的粒子群算法应用于圆度评定中,结果发现其改进的粒子群算法在圆度评定中精度得到提高;杨洋[5]等提出将改进教与学算法应用于圆度误差评定,提高了圆度误差评定精度.鲸鱼优化算法[6]是近年来由澳大利亚学者受座头鲸捕食习性启发,提出的一种新型群智能算法,该算法具有较好的稳定性和收敛性等优点,目前已广泛应用于工程应用中.为提高圆度误差评定精度,将鲸鱼优化算法应用于圆度误差评定中,并通过实验数据验证其优势。
研究设计的钢管非接触式测量平台主要是针对大口径钢管,大口径钢管一般其公称直径在500mm以上,其在工业实际测量过程中测量较为困难.为实现对大口径钢管的圆度测量,设计了一套钢管非接触式测量系统.该系统首先将上位机与ABB机器人通过socket通讯,进而实现对机器人的控制,控制ABB机器人携带高精度激光位移传感器对钢管内壁进行扫描,将激光位移传感器采集到的数据通过放大器单元和数据采集卡单元传输给上位机,上位机再对传输的数据进行数据处理,进而得到钢管截面的圆度及直径.钢管非接触式测量平台总体结构示意图如图1所示,主要硬件部分选型如表1所示.ABBGIRBG1200工业机器人是六自由度六轴工业机器人,其灵活实用,重复定位精度为0Ʊ025mm,激光位移传感器采用的是基恩士ILG300系列高精度激光位移传感器,测量范围为160~450mm,重复精度为30μm.为完全满足测量需求,搭建了测量系统实验平台,该平台系统占地长为3m,宽为3m,高为2Ʊ5m.钢管非接触式测量系统平台实物搭建图如图2所示.
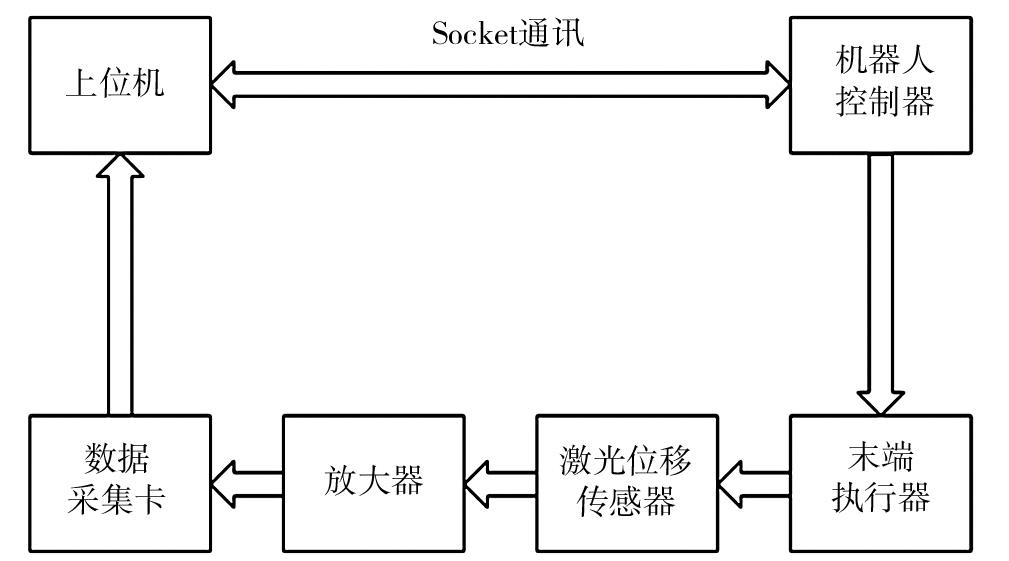
图1 钢管非接触式测量平台总体结构示意图

图2 钢管非接触式测量系统平台实体图
表1 测量平台主要硬件选型

测量系统以工业机器人为载体,采用高精度激光位移传感器对钢管内壁截面进行扫描,再经过评定算法得出钢管截面的圆度误差.测量系统的数据采集数学模型如图3所示.在图3中,O点表示测量系统机械臂工具坐标系旋转中心点;R表示机器人末端夹具测量臂的固定长度;Di表示机器人末端以旋转中心等间距角θ旋转后激光位移传感器测的距离;P点表示激光位移传感器进行测量的第一个测量位置点;Q点表示机械臂末端以旋转中心等间距角θ旋转后在直角坐标系下的第i个位置点;Li表示激光位移传感器测量的第i个位置点时的总测量距离.
测量系统是以机器人末端工具坐标系原点为旋转中心进行等间距角θ旋转测量,激光位移传感器第一个发射的激光点与发射点的连线为极轴,法兰盘的旋转中心为极点,激光位移传感器的总测量距离为极径,
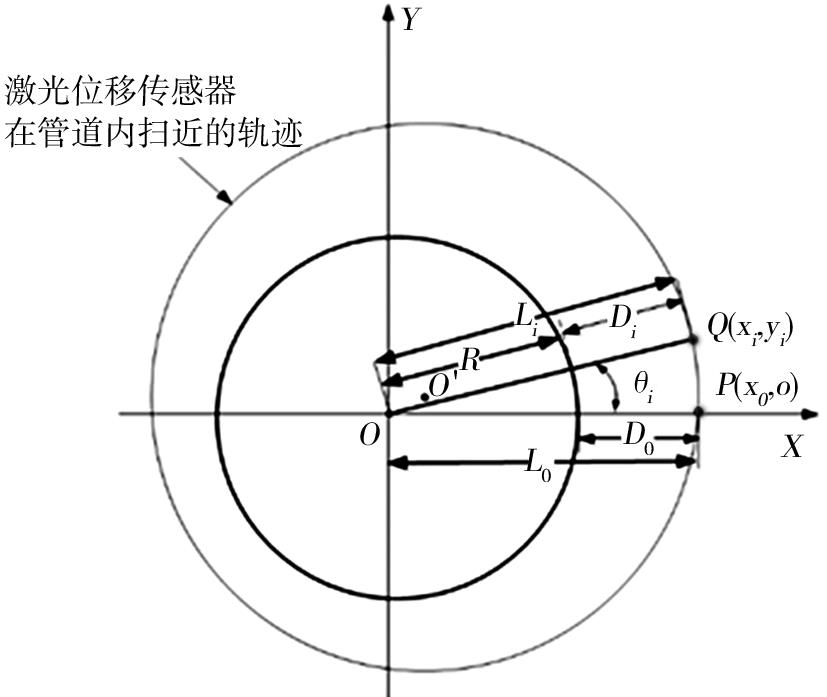
图 3 数据采集数学模型
以此建立极坐标系.当激光位移传感器在钢管内壁采集数据过程中,因其激光位移传感器的旋转平面与钢管轴线并不垂直,从而使得测量误差较大,因此须对机器人的测量姿态进行调整.首先对机器人建立工具坐标系,该工具坐标系的某一轴方向与激光位移传感器第一个发射点与激光点连线的方向一致,同时建立的工具坐标系在机械臂进行运动过程中是不断变换的,因此为了保证测量的准确性,需将建立的极坐标系转换为机器人在初始测量位置时机器人的工具坐标系.由图1可知,激光位移传感器测量的第一个位置点P时的总测量距离为:

相应的激光位移传感器测量的第i个点位置P点的总测量距离为:

将其转换至工具坐标系的二维直角坐标系下的值为:

通过激光位移传感器在钢管内壁扫过的轮廓进行算法拟合,进而得到钢管的圆度和直径测量值.
由于研究设计的大口径钢管圆度测量系统以激光位移传感器对钢管内壁进行非接触式测量,为了保证测量精度与准确性,需保证机器人末端执行器上的激光位移传感器的旋转面与钢管的轴线方向垂直,即保证机器人携带激光位移传感器沿钢管轴线平行方向进入钢管测量.但在实际工业测量中,因工业现场的复杂性,当钢管运输至测量位置点时,机器人末端执行器上的激光位移传感器的旋转面与钢管的轴线方向并不垂直,即激光位移传感器的旋转面的法向方向与钢管的轴线方向成一定的角度,从而在测量过程中需对机器人姿态进行调整,测量姿态调整方案如图4所示.机器人末端执行器携带激光位移传感器的旋转平面与钢管内壁相交的截面为椭圆,利用机器人携带激光位移传感器在钢管内壁沿工具坐标系的Z轴方向做线性运动,从而得到N组椭圆截面,根据激光位移传感器采集的数据对各组截面进行椭圆拟合,进一步得到椭圆拟合方程,从而得到椭圆中心坐标,将这些椭圆中心点拟合成空间直线,该直线即为钢管的理想轴线,进一步可得钢管轴线的方向向量.在机器人的测量姿态调整过程中,实质上是对建立的工具坐标系的姿态进行调整,机器人携带激光位移传感器测量时的位置并没有发生变化,因机器人携带激光位移传感器的前进方向与建立的工具坐标系的Z轴重合,因此其工具坐标系的Z轴方向向量为[0,0,1]T,从而通过机器人坐标系的转换关系,实现机器人测量姿态调整.
利用最小二乘法[7]对激光位移传感器采集的数据进行椭圆拟合,设椭圆的一般式:
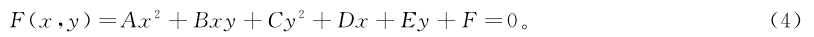
将激光位移传感器在钢管内壁以等间距角θ进行旋转,得到N组坐标数据,将这些含有坐标误差的坐
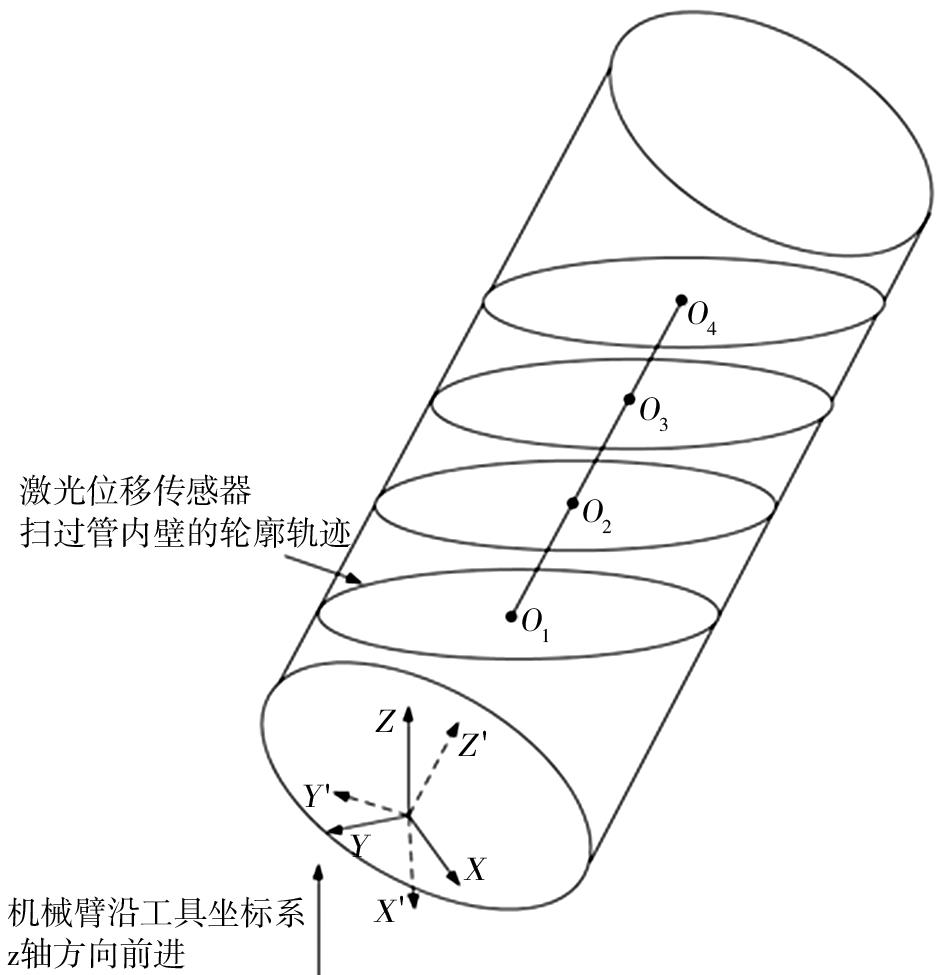
图4 机器人的测量姿态调整方案图
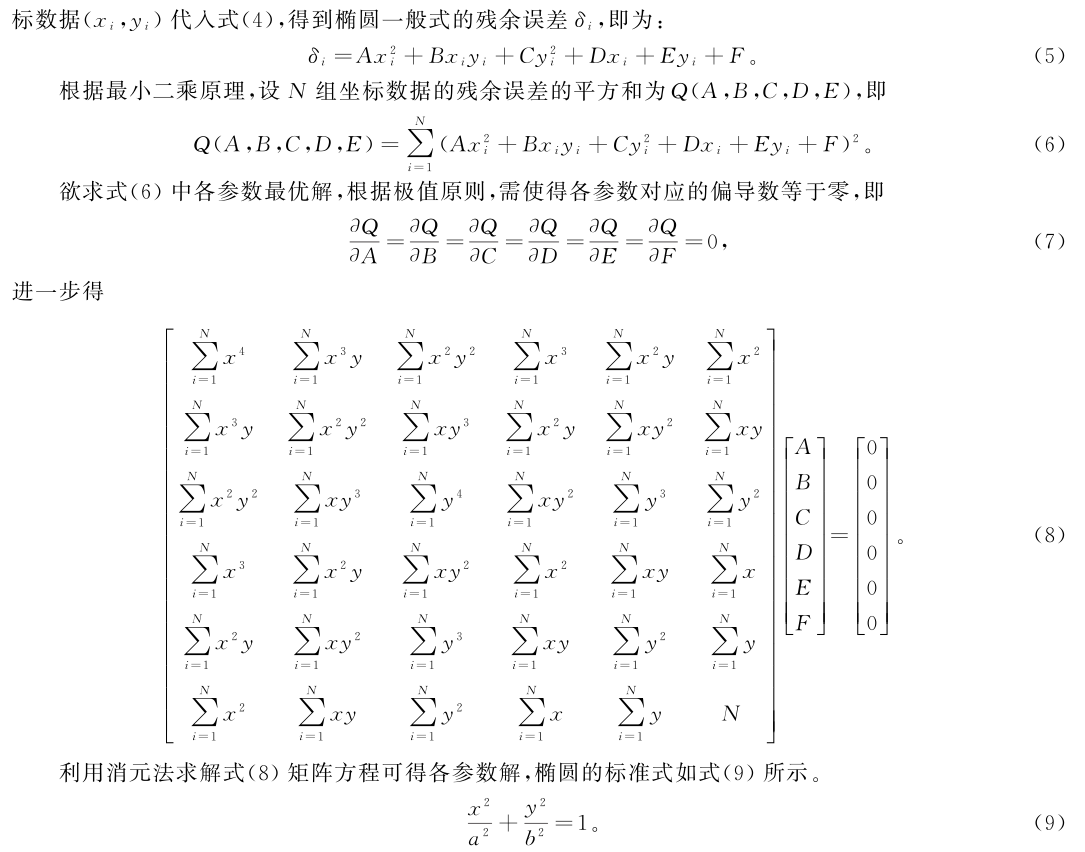
将椭圆标准式与一般式进行转换,其转换式为:
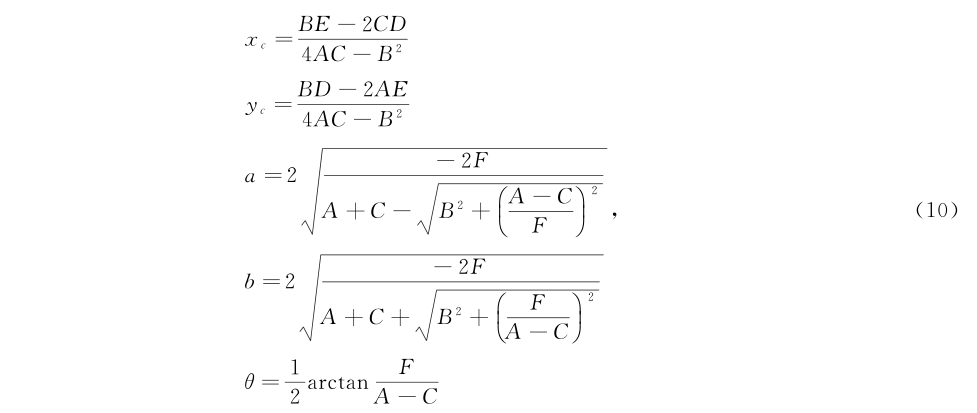
式中,(xc,yc)为椭圆几何中心;a,b分别为椭圆长短半轴;θ为椭圆长轴倾角.根据式(8)、式(10)可求出激光位移传感器扫过钢管内壁的各椭圆截面的几何中心坐标.再利用最小二乘法将各椭圆截面的几何中心进行空间直线拟合,进而得到钢管理想轴线的方向向量.设空间直线方程[8]为:

经过式(14)可解出空间直线方程的各参数G,H,I,J的值,从而得到钢管轴线所在的空间直线方程的方向向量.
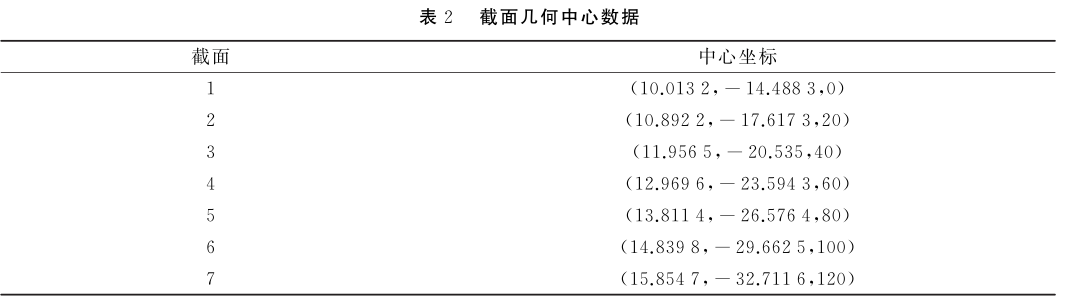
设计的钢管非接触式测量系统采用激光位移传感器在钢管内壁扫七组椭圆截面,利用最小二乘法进行椭圆拟合得到七组椭圆的几何中心坐标如表2所示.
表2 截面几何中心数据
将七组椭圆几何中心坐标利用最小二乘法空间直线拟合,进而得到钢管轴线方程为:

由式(11)、式(12)得到空间标准形式:
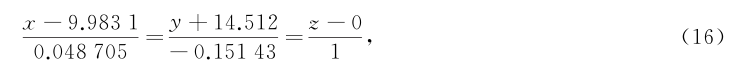
从而可得到钢管轴线方向向量为[0Ʊ048705,-0Ʊ15143,1]T
机器人的姿态描述有三种:旋转矩阵法、欧拉角法、四元数法.因在机器人姿态调整过程中只需对机器人的工具坐标系进行姿态调整,即可实现机器人携带激光位移传感器沿着钢管轴线平行方向进行测量.方案采用的是欧拉角法的变换方式,因在姿态调整中只需对机器人的工具坐标系的X轴方向和Y轴方向进行旋转相应的欧拉角,Z轴方向无需进行旋转角度,即可使得激光位移传感器沿着钢管轴线平行方向进行测量.同时因建立的机器人工具坐标系的Z轴方向与机器人携带激光位移传感器进行线性运动的方向一致,从而其方向向量为[0,0,1]T,记为向量A,钢管轴线所在的空间直线方程的方向向量记为B.方案采用常用的ZYX欧拉角[9]进行旋转变换,机器人坐标系变换公式如式(17)所示.
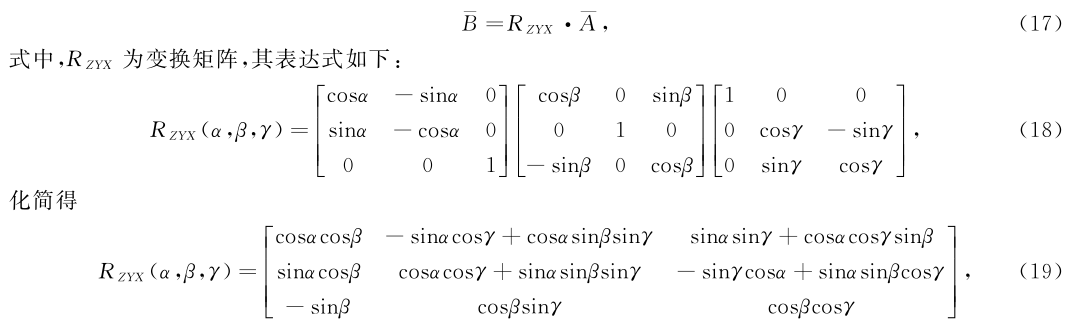
式中,α为Z轴对应的调整欧拉角;β
为Y轴对应的调整欧拉角;γ为X轴对应的调整欧拉角.因机器人在调整测量姿态时,只需将工具坐标系的X轴方向和Y轴方向旋转相应的欧拉角而Z轴无需转动,即可使得激光位移传感器沿着钢管轴线平行方向进行测量,因此对应的α=0.
机器人测量姿态调整步骤:①对机器人进行校零,建立工具坐标系;②上位机控制机器人携带激光位移传感器进行等间距角旋转,在钢管内壁扫描椭圆截面,当机器人第六轴旋转360°后,机器人沿工具坐标系Z轴做线性运动,进行下一个椭圆截面扫描,重复该步骤直到达到要求的截面数为止;③上位机对激光位移传感器采集的数据进行椭圆拟合,得到椭圆几何中心坐标,再将N组椭圆截面的几何中心坐标进行空间直线拟合,得到钢管轴线方程,进一步得到钢管轴线方向向量;④上位机计算机器人工具坐标系的X轴与Y轴的姿态调整量,输入机器人;⑤机器人进行测量姿态调整,调整完毕后再执行②~④步骤,再次计算X轴和Y轴的姿态调整量,如果计算的调整量在0Ʊ5°以内,则调整完毕,若超过0Ʊ5°,则继续执行步骤②~④,直至调整完毕.由2.2节可知轴线的方向向量B=[0Ʊ048705,-0Ʊ15143,1]T,代入式(19)得
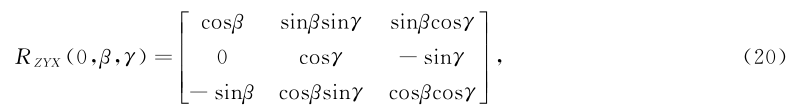
代入式(17)得β=2Ʊ788387485°,因此机器人只需沿着ZYX的调整顺序进行调整相应的欧拉角,即可使激光位移传感器沿着钢管内壁轴线平行方向进行测量,各轴调整的欧拉角为:Z轴需调整0°,Y轴需调整2Ʊ788387485°,X轴需调整8Ʊ709806245°.
WOA算法主要有3个阶段:包围捕食阶段、螺旋气泡捕食阶段、随机捕食阶段.(1)座头鲸在捕食猎物时,若随机概率P<0Ʊ5,同时收敛因子A的模小于1,则座头鲸采取收缩包围捕食,在收缩包围捕食时,座头鲸向着离猎物最近的座头鲸移动进行更新自身位置,公式为:

研究采用最小区域原则对圆度误差进行评定,圆度误差评定有四种方法:最小区域圆法、最小二乘圆法、最大内切圆法及最小外接圆法.其中,最小区域圆法的评定精度最高,是国际标准中唯一认可的评定方法.圆度误差评定实质上是非线性优化问题,而传统的计算方法在计算非线性优化问题上不易求解,考虑到智能算法求解非线性优化问题较为方便,因WOA算法需调整参数少、稳定性较好,故采用WOA算法根据最小区域法原则进行圆度误差评定.最小区域圆法是根据实际圆轮廓点得到两个同心圆,这两个同心圆都包含所有的轮廓点且两同心圆的半径差最小,两个同心圆的半径差即为圆度误差,圆度误差示意图如图5所示.在找寻满足包含所有轮廓测量点的两个同心圆的过程主要是对同心圆的圆心O(ai,bi)进行寻优,因满足包含所有测量轮廓点的同心圆有无数个,但要使两个同心圆的半径差值最小的却只有一个.实际测量轮廓点坐标Q(xi,yi)值到圆心的距离Ri的数学表达式如下:
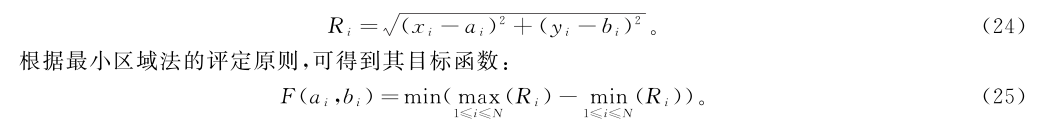
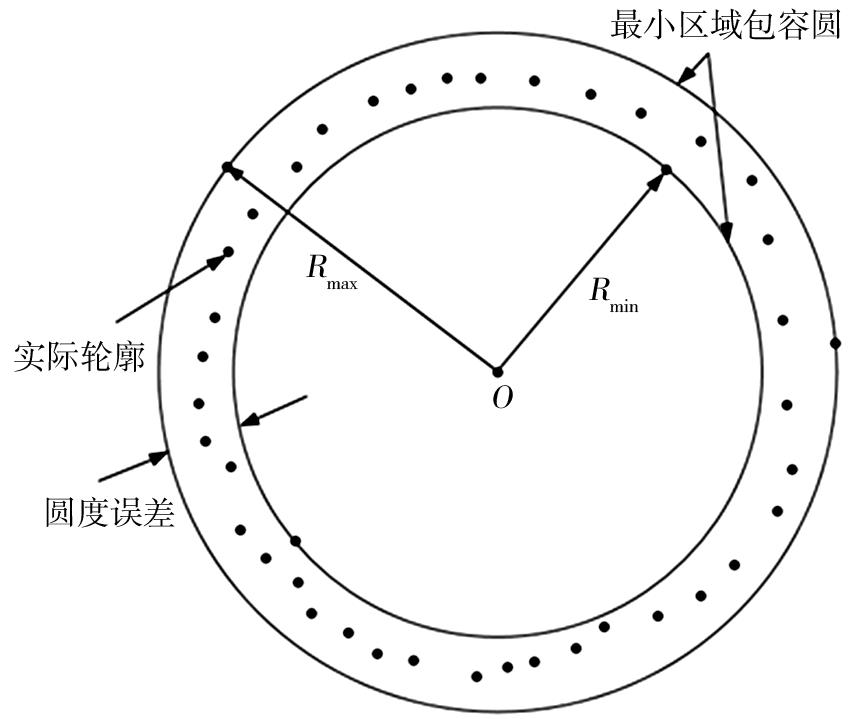
图5 圆度误差示意图
步骤1:设定算法相关参数:设定算法最大迭代次数T=100;种群规模S=50;优化变量上下限ub、lb,其区间为[-50,50];螺旋系数b=1;算法变量维数D=2以及定义目标函数F(ai,bi).
步骤2:根据式(26)产生随机数,再根据式(25)计算每个座头鲸的适应度值,保存最优的个体X∗;

步骤3:当迭代次数小于最大迭代次数时,对A,C,P,l,a进行更新;判断产生的随机数P是否大于0Ʊ5和|A|是否大于1,当P<0Ʊ5,且|A|<1时,根据式(21)更新座头鲸的位置;当|A|≥1时,根据式(23)更新座头鲸位置;若P≥0Ʊ5,根据式(22)更新座头鲸位置.
步骤4:根据式(25)计算每个座头鲸的适应度函数值,保存最优的鲸鱼个体.
步骤5:判断迭代次数是否达到最大迭代次数,若是,则输出最优解,即为圆度误差值,若未达到,则继续步骤3、步骤4.
为了验证WOA算法在圆度误差评定中的精度,研究以内径为800mm的无缝钢管为测量对象,利用设计的钢管非接触式测量系统中激光位移传感器采集的数据进行测量实验,机器人携带激光位移传感器以每2°进行旋转,在钢管内壁某一截面进行数据采集,共采集到180个测量点,将采集到的180个测量点坐标利用WOA算法进行圆度误差评定,并将WOA算法的圆度误差评定结果与最小二乘法、遗传算法(GA)进行对比.
对采集到的180个测量点数据分别采用WOA算法、GA算法进行圆度误差评定,设定最大迭代次数都为150次,种群规模都为35,并各进行40次独立运行,得出的圆度误差值取平均值.为了便于显示采用智能算法在圆度评定中的优势,并将工业中圆度误差评定中常用的最小二乘圆法求得的圆度误差值与两种算法求出的圆度误差值进行对比,几种算法求出的圆度误差值取平均值后的计算结果如表3所示.为了对比两种算法的圆度误差评定结果的稳定性,将两种算法的40次运行得出的圆度误差值进行对比,得到两种算法圆度评定结果稳定性对比图如图6所示,对应的平均收敛曲线对比图如图7所示.从表3、图6和图7可以看出,WOA算法的圆度评定结果精度相对来说最高,稳定性也更好,收敛速度也相对较快.以上均验证出WOA算法能正确有效地应用于圆度误差评定.
表3 不同算法的圆度误差计算结果

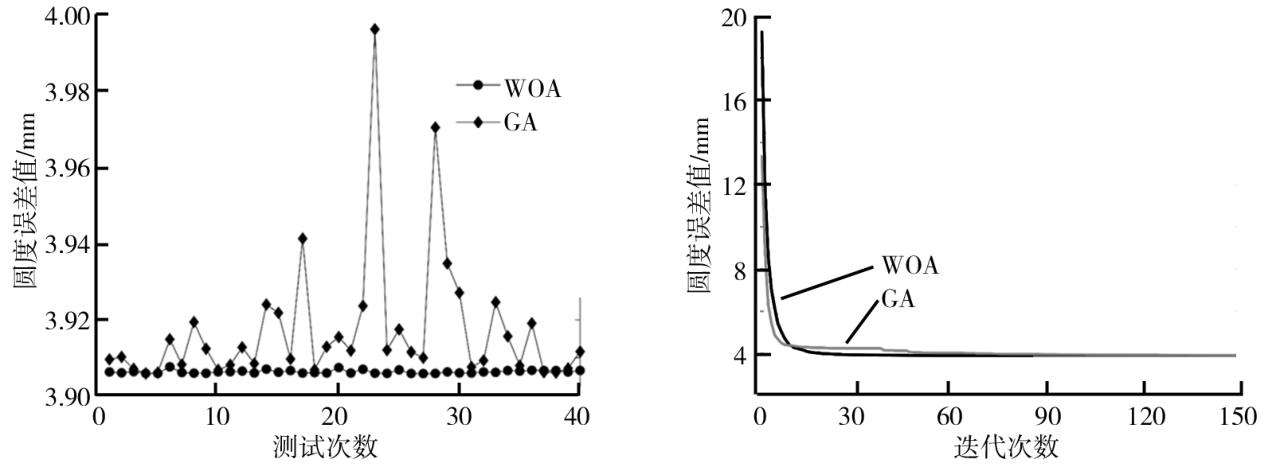
图6WOA与GA圆度评定结果稳定性对比图 图7 对应的平均收敛曲线对比图
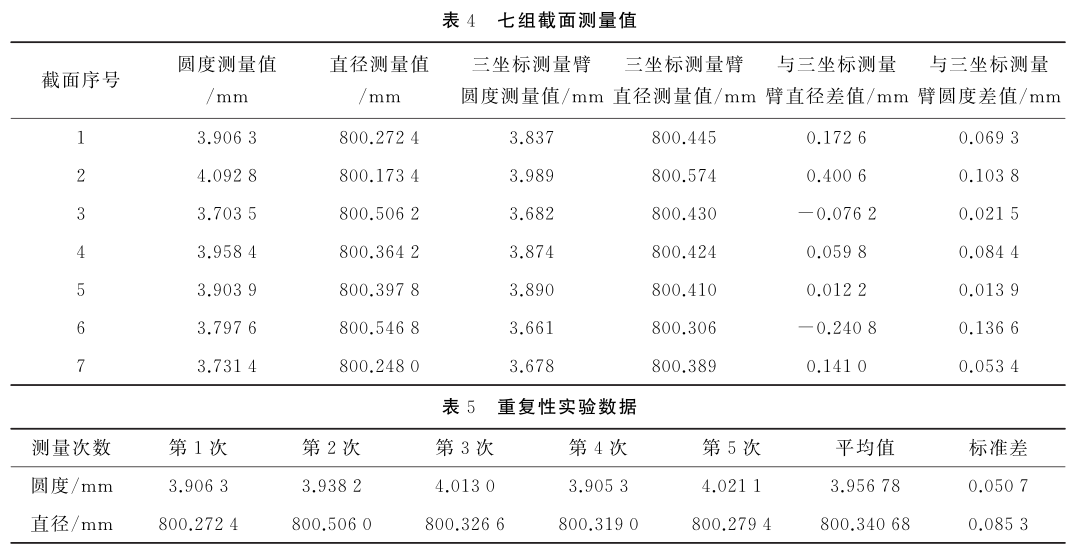
利用搭建的钢管非接触式测量实验平台,对被测钢管七组截面利用WOA算法进行圆度误差评定实验,并以三坐标测量臂对这七组截面进行圆度误差评定的结果为标准,测量评定结果如表4所示.从表4可以看出,设计的测量实验平台的圆度误差测量值与三坐标测量臂的测量值接近,误差较小.为了验证设计的钢管非接触式测量平台的圆度误差测量的稳定性,对同一个截面进行5次重复性实验,测量结果如表5所示.从表5可以看出,系统稳定性较好,能满足实际测量需求.
表4 七组截面测量值 / 表5 重复性实验数据
研究设计的钢管非接触式测量系统,采用工业机器人携带激光位移传感器对钢管内壁进行非接触式测量,并提出了该系统中机器人测量姿态调整方案,使得激光位移传感器能沿钢管轴线平行方向进行测量,有效地提高了系统测量的准确性,减小了测量误差.通过对被测钢管的七组截面进行圆度误差评定实验和系统的重复性实验,得出测量系统的测量结果与三坐标仪的测量结果接近,同时系统的重复性较好,能满足实际测量需求.研究还提出将WOA算法应用于圆度误差评定,通过试验验证得出,在圆度误差评定中,相对于GA算法和最小二乘圆法,WOA算法在精度、稳定性以及收敛速度方面都具有优势.
[1]钟锡弟.2019年我国钢管行业现状与前景预测[J].钢管,2019,48(4):1G5.
[2]王宸,向长峰,王生怀.改进天牛须搜索算法在圆度误差评定中的研究[J].制造技术与机床,2019(11):143G146.
[3]罗钧,林于晴,刘学明,等.改进蜂群算法及其在圆度误差评定中的应用[J].机械工程学报,2016,52(16):27G32.
[4]崔星星,陈岳坪,卢海燕.改进的粒子群算法在圆度误差评价中的应用[J].机械设计与制造,2015(4):88G90,94.
[5]杨洋,李明,顾京君,等.改进教与学算法在圆度误差评定中的应用[J].机械设计与制造,2019(5):117G120.
[6]SEYEDALIMIRJALILI,ANDREWLEWIS.Thewhaleoptimizationalgorithm[J].Advancesinengineeringsoftware,2016,95:51G67.
[7]陈若珠,孙岳.基于最小二乘法的椭圆拟合改进算法研究[J].工业仪表与自动化装置,2017(2):35G38,46.
[8]袭杨.空间直线拟合的一种方法[J].齐齐哈尔大学学报,2009,25(2):64G68.
[9]李永超.飞机壁板机器人自动化制孔法向修正技术研究[D].杭州:浙江大学,2014.
[10]崔东文.鲸鱼优化算法在水库优化调度中的应用[J].水利水电科技进展,2017,37(3):72G76,94.
[11]刘思遥,黄美发,冯建国,等.基于自适应多种群遗传算法的圆度误差评定[J].组合机床与自动化加工技术,2016(8):96G99.

